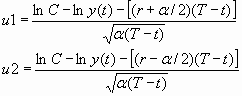We assume a derivative V(y(t),t) that depends on time t and an underlying asset y(t). The derivative is due at time T. The risk less interest rate is represented by r.
The fair price of the option is the discounted expectation value of the option at the end of the period (T-t).
The asset y(t) will be modeled by a geometric Wiener process as introduced in the previous chapter.
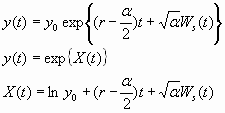
Thereby X(t) denotes the Wiener process with drift.
Let us assume V(y(t),t) is a European call option with the exercise price C than the following transformation holds true:
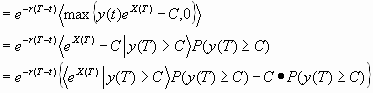
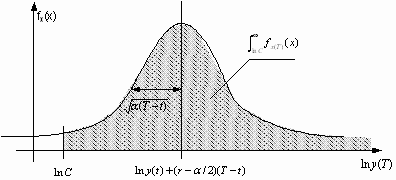Thereby fx(x) is the probability distribution function of the Wiener process with drift (b
y-a
/2) which gives the distribution for the logarithmic asset value [ln y(T)] at the time T when the option matures.
The term
can be transformed into a normal density distribution depending on x with a drift (b
y+a
/2) by separating the term
which no longer depends on x.
This allows for introducing F (u) the standard distribution function.
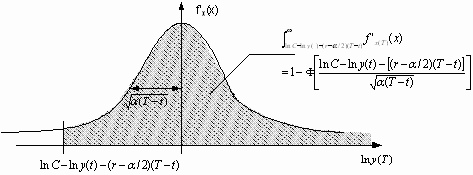
In addition we use the fact that the distribution is symmetric and the total integral is one. This means F (-u) equals 1-F (u) which leads us to the Black-Scholes formula:
